VEDIC MATHS-15

 

VEDIC MATHS

                           By OMKAR TENDOLKAR

Hello friends,

                      This is our 15th blog from the series of "Vedic maths" blogs. Here in this blog we will learn about "Criss-Cross System of Multiplication".

Criss-Cross System of Multiplication :

               In Vedic Mathematics , we have similar system as like traditional way of multiplication it helps us to get the answer much faster. This system is also universal system and can be used for any combination of numbers of any length.

                     This system of Multiplication is given by the "Urdhva-Tiryak Sutra." It means 'vertically and cross-wise'. The application of this system are manifold, but in this blog we shall confine our study only to it's utility in multiplying numbers. We shall call it the criss-cross system of multiplication.

Reference:

We had already learn about "Criss-Cross System of Multiplication for 2-digit number" our previous blog. If you have missed my last blog then please visit "VEDIC MATHS-14".

 

Method:

Here in in this blog we will learn about "Criss-Cross System of Multiplication for 3-digit number". The astonishing fact is that for 3-digits numbers also we will use same system as we had used in 2-digits system in expanded form.

And in every case, we will be able to get answer in a single line.

Let us have a look at the multiplication process involve in multiplying a three-digits number by another three-digits number.

Let us multiply two three-digit numbers where there is no carry involved:

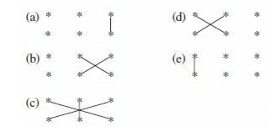
As suggested by step (b), we multiply 1 into 2 and get the answer as 2.

Next, we cross-multiply (2×2) and add it to (1×0). Thus, the final answer is 4.

In step (c), we multiply (1×2) and (2×0) and (3×1). We add the three answers thus obtained to get final answer 5.

In step (d), we multiply (1×0) and (3×2). the  final answer is 6.

    

In step (e), we Multiply the left-hand most digits (1×3) and get the answer as 3.

This, it can be seen that the product obtain by multiplying two 3-digits number can be obtained in just one line with the help of the Criss-Cross system.

More examples:

1. 121×123=14883
2. 210×121=25410
3. 111×123=13653
4. 100×201=20100
5. 112×223=24976

                Thus, we see how to Criss-Cross system of multiplication helps us get our answer in just one line! And, the astonishing fact is that this same system can be expanded to multiplication of numbers of higher digits too.

                 And in every case, we will be able to get answer in single line.         

                The simplicity of this method can be vouched from examples given above.

You may try following example:

1) 231 × 111

2) 131 × 121

3) 123 × 201

You may answer this in comment box. You may ask your any query or doubt in comment box. I will try to resolve as early as possible.

In next blog we will discuss about "Criss-Cross System of Multiplication for 3-digit number where there is carry over involved".     

Are you excited for this?...

Then, please wait for it.

I will post my new blog in next week.

We will meet very soon through our next blog. Till that stay connected, stay healthy and stay safe.

Thanks

for giving your valuable time.

Good day😊.