VEDIC MATHEMATICS

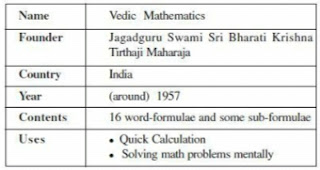
VEDIC MATHS                             By OMKAR TENDOLKA R Hello friends,                       This is  post number 100 from the series of "Vedic maths" blogs. Here in this blog we will learn about   " Applications of the Sutras & Sub-sutras " HISTORY VEDIC MATHEMATIC  : History of Vedic Mathematics Applications of the Sutras : Applications of the Sub-Sutras : We will meet very soon through our next  blog. Till that stay connected, stay healthy and stay safe. Thanks for giving your valuable time. Good day😊

  VEDIC MATHS                             By OMKAR TENDOLKA R Hello friends,                       This is  post number 99 from the series of "Vedic maths" blogs. Here in this blog we will learn about   " Raising to Fourth and Higher Powers-III " Reference: We had already learn about " Method Of Finding Cubes "  in our previous blogs. If you have missed my last blog then please visit   " VEDIC MATHS-50 " to " VEDIC MATHS-52 " . We had already learn about " Raising to Fourth and Higher Powers-I "  in our previous blogs. If you have missed my last blog then please visit   " VEDIC MATHS-97 ". We had already learn about " Raising to Fourth and Higher Powers-II "  in our previous blogs. If you have missed my last blog then please visit   " VEDIC MATHS-98 ". Raising a Number to the Fourth Power : Example: 1. Say we have to find (32)^4.  Here a is 3 and b is 2.  Step 1: We raise a to the power of 4, whic

    VEDIC MATHS                             By OMKAR TENDOLKA R Hello friends,                       This is  post number 98 from the series of "Vedic maths" blogs. Here in this blog we will learn about   " Raising to Fourth and Higher Powers-II " Reference: We had already learn about " Method Of Finding Cubes "  in our previous blogs. If you have missed my last blog then please visit   " VEDIC MATHS-50 " to " VEDIC MATHS-52 " . We had already learn about " Raising to Fourth and Higher Powers-I "  in our previous blogs. If you have missed my last blog then please visit   " VEDIC MATHS-97 ". Raising a Number to the Fourth Power : Example: 1. Say we have to find (13)^4.  Here a is 1 and b is 3.  Step 1: We raise a to the power of 4, which means (1)^4 = 1. This 1 is the first digit. We  put it down like this: 1. Step 2: We then multiply the subsequent digits by 3 as b/a is 3/1 = 3.  So our first line looks like this: 1 

   VEDIC MATHS                             By OMKAR TENDOLKA R Hello friends,                       This is  post number 97 from the series of "Vedic maths" blogs. Here in this blog we will learn about   " Raising to Fourth and Higher Powers-I " Reference: We had already learn about " Method Of Finding Cubes "  in our previous blogs. If you have missed my last blog then please visit   " VEDIC MATHS-50 " to " VEDIC MATHS-52 ". Raising a Number to the Fourth Power : The method to raise a number to the fourth power is very much like the method  of cubes. So let’s see what (a + b) is when raised to the power 4. For example,  3^4 = 81 5^4 = 625. (a + b)^4 = (a)^4 + 4 (a^3) b + 6 (a)^2 (b)^2 + 4 a (b^3) + (b)^4 The expression on the RHS can be broken into two parts as given below. The first part has the terms a^3, a^2b, ab^2, and b^3 and the second part has the terms 2a^2b and 2ab^2.     (a)^4 +   (a^3) b +   (a)^2 (b)^2  +    a (b^3) + (b)^4

  VEDIC MATHS                             By OMKAR TENDOLKA R Hello friends,                       This is  post number 96 from the series of "Vedic maths" blogs. Here in this blog we will learn about   " Quadratic Equations-III " Reference: We had already learn about " Quadratic Equations-I "  in our previous blog. If you have missed my last blog then please visit   " VEDIC MATHS-94 ". We had already learn about " Quadratic Equations-II "  in our previous blog. If you have missed my last blog then please visit   " VEDIC MATHS-95 ". Special Case of Quadratic Equations—Reciprocals: Case C 1. Here we have our first sum: x - 1/x = 5/6. Here again we have to be careful, because there is a minus sign. So we find  the factors of 6, which are 1, 2, 3 and 6. We can’t use 1 and 6, because they  don’t give us ; so we take 2 and 3 as reciprocals. Since 3/2 is greater than 2/3, we  put that first and we have the right-hand side as .  So h

  VEDIC MATHS                             By OMKAR TENDOLKA R Hello friends,                       This is  post number 95 from the series of "Vedic maths" blogs. Here in this blog we will learn about   " Quadratic Equations-II " Reference: We had already learn about " Quadratic Equations-I "  in our previous blog. If you have missed my last blog then please visit   " VEDIC MATHS-94 ". Quadratic Equations: Here in this post we will learn  how to solve quadratic equations using Vedic maths. Special Case of Quadratic Equations—Reciprocals: Case A 1. Here we have our first sum: x + 1/x = 17/4. left-hand side is the sum of two reciprocals, so we’ll simply split 17/4 the on the right-hand side into 4 + 1/4. And what we get is x = 4 or 1/4 . Answer: x = 4  or x = 1/4 . 2. Here we have our first sum: x + 1/x = 26/5. left-hand side is the sum of two reciprocals, so we’ll simply split 26/5 the on the right-hand side into 5 + 1/5. And what we get is x = 

VEDIC MATHS                             By OMKAR TENDOLKA R Hello friends,                       This is  post number 94 from the series of "Vedic maths" blogs. Here in this blog we will learn about   " Quadratic Equations-I " Quadratic Equations: Here in this post we will learn  how to solve quadratic equations using Vedic maths. Quadratic equations are of the form:   a(x)^2 + bx + c = 0 Quadratic means ‘two’. So here the unknown variable x will have two values. Here we have the formula for solving the quadratic equation as: (-b±√(b²-4ac))/(2a) . Examples : 1. Here we have our first sum: 7(x)^2 - 5x - 2 = 0 Here a = 7, b = -5 and c = -2. So we apply the formula  (-b±√(b²-4ac))/(2a)  Here, the differential is the square root of the discriminant. So we’ll get  ______________ 14x - 5 =   ±  √  25 - ( 4  ×  7  ×  -2) 14x - 5 =  ± ( 81)^1 / 2 14x - 5 =  ± 9 x =   (9 +5) / 14 = 1 . x = (-9 + 5) / 14 = 2/7 . Answer: x = 1 & x =  2/7 . 2. Here we have our first sum: 6