VEDIC MATHS-25

-

 

VEDIC MATHS

                           By OMKAR TENDOLKAR

Hello friends,

                      This is  blog number 25 from the series of "Vedic maths" blogs. Here in this blog we will learn about "how to calculate cube-root of perfect cubes along with example part-1"

Calculating cube root of numbers by traditional method is cumbersome procedure, but the technique used by Vedic Mathematics is so fast that one can get the answer in two to three seconds!

The technique for solving cube roots is simply so amazing that the student will be able to correctly predict the cube root of a number just by looking as it and without the need for any intermediate steps.

At this point, I would like to make a note that the technique provided in this blog can be used to find cube root of perfect cubes only. It can't be used to find the cube root of imperfect cubes.

Reference:

We had already learn about "concept relating to Cube-root" our previous blog. If you have missed my last blog then please visit "VEDIC MATHS-23".

We had already learn about "Method for calculating cube root of perfect number" our previous blog. If you have missed my last blog then please visit "VEDIC MATHS-24"

Solving cube roots:

We will be solving the cube roots in 2 parts. First, we shall solve right hand part of the answer and then we shall solve left hand part of the answer. If you wish you can solve left hand part before the right hand part. There is no restrictions on either method but generally people prefer to solve right hand part first.

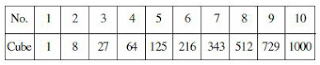
1. Find Cube root of 287496

  1. We shall represent the number 287496 as 287|496
  2. Next, we observe that the cube 287496 is ending with 6 and we know that when cube ends with 6 and we know that when the cube ends with a 6, the cube roots also ends with 6. The answer at this stage is __6. We have thus got the right hand part of our answer.
  3. To find the left hand part of the answer we take the number which lies to the left of slash. In this case, the number lying to the left of slash is 287. Now, we need to find two perfect cubes between which the number 287 lies in the number line. From the key, we find that 287 lies between the perfect Cube 216 (the cube of 6) and 343 (the cube of 7).
  4. Now out of the number obtained above, we take the smaller number and put it on the left hand part of the answer. Thus, put of 6 and 7, we take the smaller number 6 and put it beside the answer of __6 already obtained. Our final answer is 66. Thus, 66 is Cube-root of 287496.

Answer:

Cube-root of 287496 is 66.


2. Find Cube-root of 205379

  1. We represent 205379 as 205|379
  2. The cube ends with a 9, so the cube-root also ends with a 9. (The answer at this stage is __9)
  3. The part to the left of the slash is 205. It lies between perfect Cubes 125 (The cube of 5) and 216 (the cube of 6)
  4. Out of 5 and 6, the smaller number is 5 and so we take it as left part of the answer. The final answer is 59.

Answer:

Cube-root of 205379 is 59.


3. Find Cube-root of 830584

  1. The cube ends with 4 and cube root will also end with a 4.
  2. 830 lies between 729 (The cube of 9) and 1000 (The cube of 10)
  3. Since, the smaller number is 9, the final answer is 94.

Answer:

Cube-root of 830584 is 94.


You will observe as we proceeded with the examples, we took much less time to solve the cube-roots. After some practice you will be able to solve the cube-roots by simply observation of cube and without necessity of doing any intermediate steps.

It must be noted that immaterial of the number of digits in the cube, the procedure for solving them is in next blog.

More examples:
Find Cube-root of following:

  1. Cube root of 74088 is 42
  2. Cube root of 103823 is 47
  3. Cube root of 175616 is 56
  4. Cube root of 474552 is 78
  5. Cube root of 592704 is 84
The simplicity of this method can be vouched from examples given above.


You may try following example:

Find Cube-root of followings

1. 54872

2. 110592

3. 830584

You may answer this in comment box. You may ask your any query or doubt in comment box. I will try to resolve as early as possible.

In next blog we will discuss about "how to calculate cube-root of perfect cubes along with example part-2".     

Are you excited for this?...
Then, please wait for it.
I will post my new blog in next week.

We will meet very soon through our next blog. Till that stay connected, stay healthy and stay safe.

Thanks

for giving your valuable time.

Good day😊.

Comments

Post a Comment

Popular posts from this blog

VEDIC MATHEMATICS

-
Image
  VEDIC MATHS                             By OMKAR TENDOLKAR Hello friends,                        I am Omkar Tendolkar from Kudal. I am studying in S.Y.B.Sc at SRM College, Kudal. I always enjoy sharing my knowledge. This is one of my attempts.            Some people find mathematics challenging to understand, while others struggle with calculations. Certainly, the comprehension of the subject depend on IQ (intelligent quotient), but equally crucial is one's perspective towards it. Because mastering calculation doesn't solely rely on a sharpe IQ; it also demands some basic tricks that can greatly assist in handling complex calculations.                  Starting today, I want to launch a "VEDIC MATHS" blog. Here, you will find a series of blog's explaining simple tricks that will...
Read more

VEDIC MATHS-1

-
Image
VEDIC MATHS                             By OMKAR TENDOLKAR Hello friends,                          This is our first blog in the series of 'Vedic Maths' blogs. Here, we will learn about the basic principles required in Vedic Maths. This blog will cover all the fundamental concepts necessary for understanding our next few blogs.   Base: It is the first number in the series. For a two-digit number: 10. Starting with 10, 100, 1000, 10000, etc. Complement: . Adding two numbers results in the next nearest base. 48 + 52 = 100. Then, We can say that 48 is the complement of 52 or 52 is the complement of 48. How to find: Subtract each digit from 9 and the last digit from 10. If... The last digit is 0, then take the second-to-last digit as the last one. For example: 60 is the complement of 40. All these examples, ranging from 2 digits to 6 digits, w...
Read more

VEDIC MATHS-15

-
Image
  VEDIC MATHS                             By OMKAR TENDOLKA R Hello friends,                       This is our 15th blog from the series of "Vedic maths" blogs. Here in this blog we will learn about   "Criss-Cross System of Multiplication " . Criss-Cross System of Multiplication :                In Vedic Mathematics , we have similar system as like traditional way of multiplication it helps us to get the answer much faster. This system is also universal system and can be used for any combination of numbers of any length.                      This system of Multiplication is given by the " Urdhva-Tiryak Sutra. " It means ' vertically and cross-wise '. The application of this system are manifold, but in this blog we shall confine our study only to it's utility in...
Read more