VEDIC MATHS-39

 

VEDIC MATHS

                           By OMKAR TENDOLKAR

Hello friends,

                      This is  post number 39 from the series of "Vedic maths" blogs. Here in this blog we will learn about "Application Digit-Sum Method-2".

Digit-Sum Method:

All the techniques that we have discussed in previous posts till now have emphasized various methods of quick calculation. They have helped us in reducing our time  in some cases provided the final answer without any actual calculation.

In this post, we will study the digit-sum method. This method is not used for quick calculation but only  for quick checking of answers. It will help us verify the answer that we have obtained to a particular question.

Although the digit-sum method is discussed by Jagadguru Bharati Krishna Maharaj in his study, mathematicians in other parts of the world were aware of this principle even before the thesis of Swamiji was published. Prof. Jackaw Trachtenberg and other mathematicians have dealt with this principle in their research work.

Reference:

We had already learn about "Digit-Sum Method" our previous blog. If you have missed my last blog then please visit "VEDIC MATHS-37".

We had already learn about "Application Digit-Sum Method-1" our previous blog. If you have missed my last blog then please visit "VEDIC MATHS-38".

Digital sum:

In the digital sum we have to convert any given number into single digit by repetitively addition up all the  digit of that number.

Short-cut to above method:

"While calculating the digit-sum of a number, you can eliminate all the nines and all the digits that add up to nine".

When you eliminate all the nines and all the digits that add up to nine you will be able to calculate the digit-sum of any number much faster. 

The elimination will have no effect on the final result.

Example:

1) Find the digit-sum of 6372819923

Firstly, we go through traditional method:

The digit sum of 6372819923 is:

6+3+7+2+8+1+9+9+2+3 = 50 and again 5+0 is 5.

here we will try short-cut method:

Now, we will eliminate the numbers that add up to 9 (6 and 3, 7 and 2, 8 and 1 and also eliminate the two 9’s)

We are left with the digits 2 and 3 which also add up to 5. 

Hence, it is proved that we can use the short-cut method for calculating the digit-sum. 

The answer will be the same in either case.

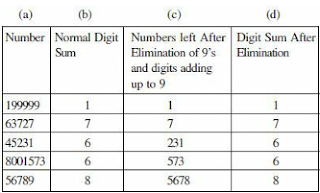
A few more examples:

.

From the above table we can see that the values in column ‘b’ and the values in column ‘d’ are similar.

Note: If the digit-sum of a number is 9, then we can eliminate the 9 straight away and the digit-sum becomes ‘zero.’

Digit-sum is useful for quick checking  of answer as follow:

The simplicity of this method can be vouched from examples given above.

You may try following example:

Verify whether the following answers are correct or incorrect without actual calculation.

1..6582170 - 9999999 = -3417829

2. 900/120 gives quotient 7 and remainder 60

3. 0.45632 × 0.65432 = 0.2985793024

You may answer this in comment box. You may ask your any query or doubt in comment box. I will try to resolve as early as possible.

In next blog we will discuss about "General Equations".     

Are you excited for this?...

Then, please wait for it.

I will post my new blog in next week.

We will meet very soon through our next  blog. Till that stay connected, stay healthy and stay safe.

Thanks

for giving your valuable time.

Good day😊.